GIS中四叉树索引及其分类介绍

在GIS中，四叉树索引又分为很多种类，包括点四叉树、PR四叉树、MX四叉树等，本文这里做一个简单的介绍。

1.点四叉树（Point Quadtree）

点四叉树与KD树相似，两者的差别是在点四叉树中，空间被分割成四个矩形。四个不同的多边形分别是：SW、NW、SE、NE。其搜索过程和KD树相似，当一个点包含在搜索范围内时被记录下来，当一个子树和搜索范围有交叠时它将被穿过。下图：点四叉树示意图

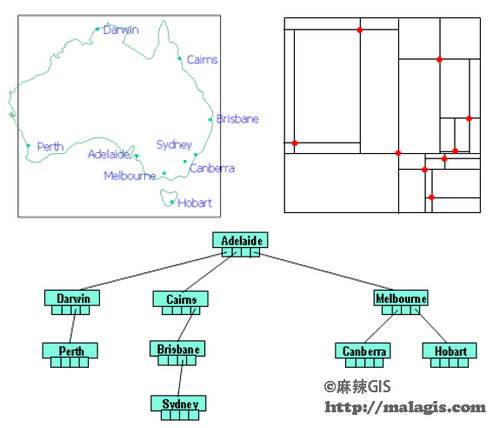
2.PR四叉树(Point Region Quadtree)

PR四叉树是点四叉树的一个变种，它不使用数据集中的点来分割空间。在PR四叉树中，每次分割空间时，都是将一个正方形分成四个相等的子正方形，依次进行，直到每个正方形的内容不超过所给定的桶量（比如一个对象）为止。下图：PR四叉树

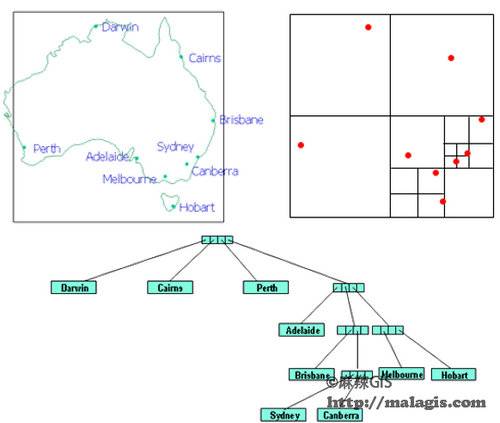
3.MX四叉树

空间被分割成四个矩形。四个不同的多边形分别是：SW、NW、SE、NE。每次分割空间时，都是将一个正方形分成四个相等的子正方形，依次进行，直到每个正方形的内容不超过所给定的桶量（比如一个对象）为止。

所有的数据都处在四叉树的同一个深度，多个点可以由一个指针联接。

4.基于固定网格划分的四叉树索引

先看下图：

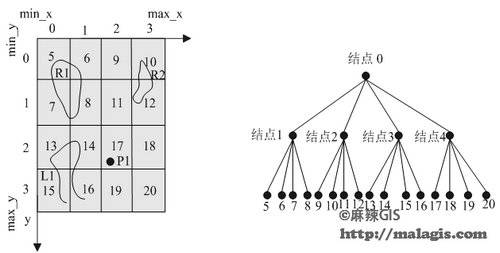
非叶结点数：MAX_NONLEAFNODE_NUM=\(\sum_{i=0}^{N-1}4^i\)

叶结点数：MAX_LEAFNODE_NUM=2^N×2^N=4N

非叶结点从四叉树的根结点开始编号：

从0到MAX_NONLEAFNODE_NUM-1

叶子结点则从MAX_NONLEAFNODE_NUM开始编号，

直到MAX_NONLEAFNODE_NUM+MAX_LEAFNODE_NUM-1

在四叉树中，空间要素标识记录在其外包络矩形所覆盖的每一个叶结点中，但是，当同一父亲的四个兄弟结点都要记录该空间要素标识时，则只将该空间要素标识记录在该父亲结点上，并按这一规则向上层推进。

5.线性可排序四叉树索引

•首先将四叉树分解为二叉树，即在父结点层与子结点层之间插入一层虚结点，虚结点不用来记录空间要素，然后按照中序遍历树的顺序对结点进行编码，包括加入的虚结点。

假设某个结点位于四叉树的第N层，可排序四叉树编码为Index。它的四个子结点位于树的第N-1层，编码从左到右分别为：

Index_C1=Index－3×4×（N－1）　

Index_C2=Index－4×（N－1）

Index_C3=Index＋4×（N－1）

Index_C4=Index＋3×4×（N－1）

通过编码值很容易确定结点在树中的层数。在进行查询时，给定一个查询范围，假定为矩形，这个矩形范围唯一的对应一个四叉树结点。通过结点的编码，可以快速计算出在这棵子树下的所有子结点。

找子结点的范围的程序伪代码如下：

GetIndexRange(long Index，long Min，long Max)
{
  long  n = GetLayerNum(Index);
  Min = Max = Index;　　　　
  While(n>0)
  {
    Min = Min－ 3×4×(n－1);
    Max = Max－3×4×(n－1);
    n = n –1;