常用地图投影之圆柱投影(cylinder projection)

圆柱投影基本概念：

根据特定的条件，将地球椭球面上的经纬线投影到圆柱面上，并沿圆柱母线切开展成平面，这种投影称为圆柱投影。

圆柱投影分类：

按变形性质分

等角圆柱投影,等面积圆柱投影和任意圆柱投影（特例：等距离圆柱投影)

按圆柱面与地球相对位置分

正圆柱投影
斜轴圆柱投影
横轴圆柱投影

正轴圆柱投影的一般公式

\[x=f(\phi)\]

\[y=\alpha\cdot\lambda\]

\[m=dx/(Md\phi)\]

\[n=\alpha/r\]

\[p=a\cdot b=m\cdot n=\alpha dx/(rMd\phi)\]

\[sin\omega/2=(a-b)/(a+b)=(m-n)/(m+n)\]

或者：

\[tg(45^{0}+\omega/4)=(a/b)^{1/2}=(m/n)^{1/2}\]

正轴等角圆柱投影（墨卡托投影）

公式：

\[x=\alpha/mod lgU\]

\[y=\alpha\cdot \lambda\]

\[m=n=\alpha/r\]

\[p=m^{2}\]

\[\omega=0\]

其中mod=0.4342945

投影常数\(\alpha\)确定

令纬度\(\phi_{k}\)上的长度比\(n_{k}=1\)

则

\[n_{k}=a/r_{k}=1\]

\[\alpha=r_{k}\]

故

割圆柱投影中，\(\alpha=r_{k}\)

当\(\phi_{k}=0\)时

切圆柱投影中，\(\alpha=a\)

等角航线（恒向线，斜向线）

是地面上两点之间的一条特殊的定位线，是两点间与所有经线处处成相同方位角的一条曲线。

等角航线在地图上的表象为两点之间的直线
\[tg\alpha=(y_{2}-y_{1})/(x_{2}-x_{1})\]

如图所示：

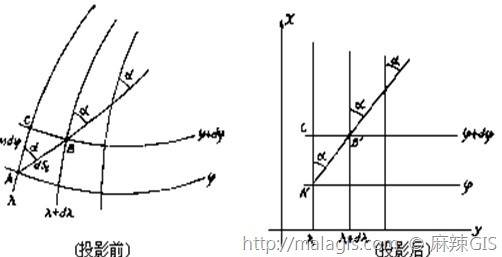
圆柱投影变形分析及其应用

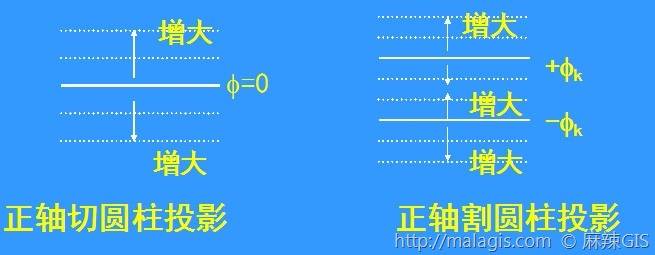
适用范围：

低纬度处沿纬线延伸的地区。对于沿经线延伸的地区：采用横轴圆柱投影。