「GIS算法」道格拉斯普克(Douglas-Peuker)算法原理图解

道格拉斯-普克算法（Douglas–Peucker algorithm），也称为拉默-道格拉斯-普克演算法（Ramer–Douglas–Peucker algorithm），从名字就可以看出这个算法是谁提出的，是GIS系统中用于简化曲线的一种常用算法。算法最初由拉默（Urs Ramer）于1972年提出，1973年道格拉斯（David Douglas）和普克（Thomas Peucker）二人又独立于拉默提出了该算法。

PS：看看GIS的前辈们有多卷，一个算法三个人发现了三次，名字都要用三个人的。

算法作用

在GIS系统中如何存储一条曲/折线？常见的方式就是使用使用一系列坐标点的集合来表示，点越多越密集，那么所能表示的精度就越高。在GIS画图的时候理想状况下，我们当然希望精度越高越好，但高精度的数据也会带来一些问题，比如对硬件系统的要求变高；比如在一些可视化场景里造成的渲染问题。

道格拉斯-普克算法正是用来解决这些问题的，它可以在保证一定精度的前提下，简化曲线的绘制过程，也是目前被广泛应用的GIS算法。基于线状实体的点压缩算法，用来压缩简化矢量数据。

算法流程

1. 输入一系列坐标点组成的曲线。
2. 曲线第一个点A和最后一个点B连成一条直线AB。
3. 确认一个阈值（这个值用于控制简化后曲线的精度）
4. 分别计算曲线上各点到这条直线的距离，并取出其中的最远距离与阈值进行比较。
5. 如果最远距离大于阈值，则将该点保留，记为C，此时可以生成两条直线AC、CB，重复步骤4
6. 否则将该点舍弃。

这么描述的有点抽象，我们还是看百科里给的动图。

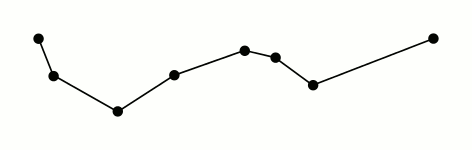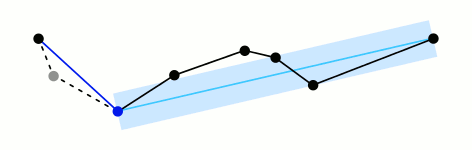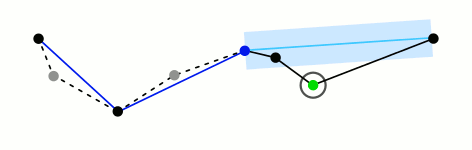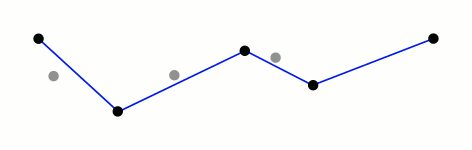
图解

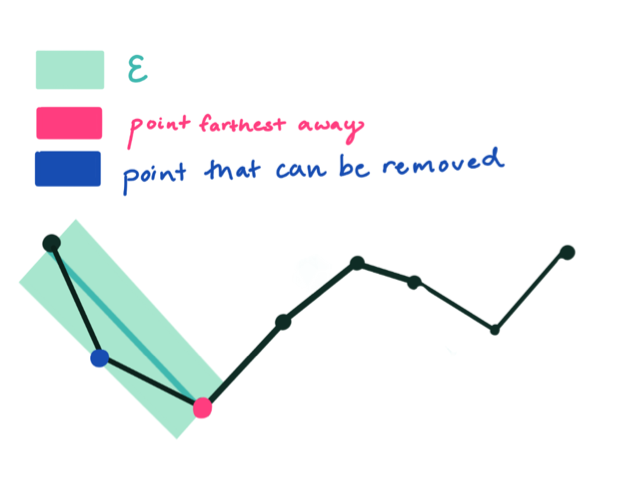
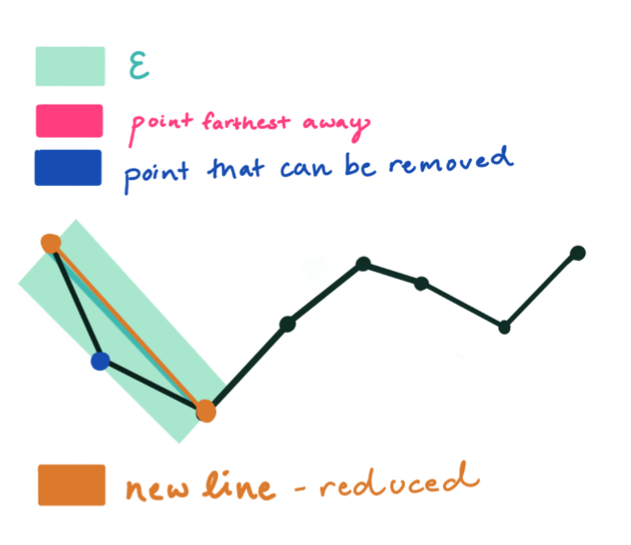
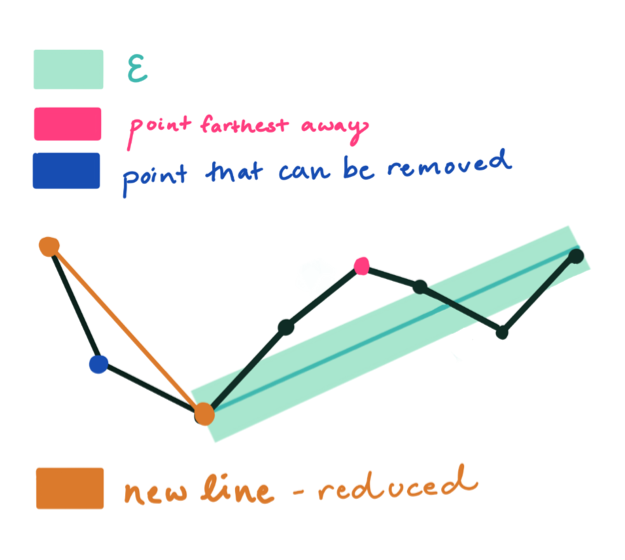
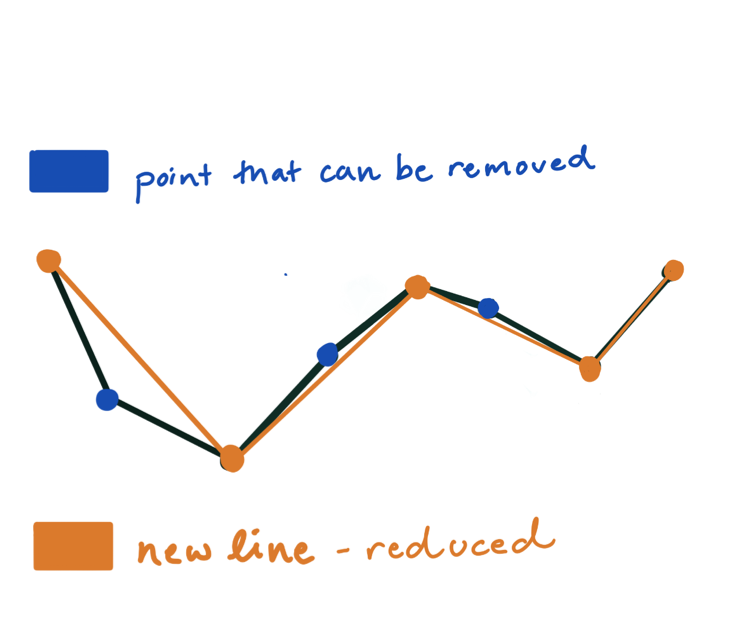
这个绿色的宽度就代表阈值，红色代表每次算法中最远的点，蓝色表示可以被移除的点，橙色表示最后生成的曲线。

参考

1. 道格拉斯-普克算法 - 维基百科，自由的百科全书

2. The Algorithm That Ties Together Google Maps and InfluxData’s Giraffe – The New Stack

3. 道格拉斯普克(Douglas-Peuker)算法及python实现