制图综合的方根模型（开方根规律）

概念

开方根规律是由德国特普费尔提出的一种制图综合的方案，用于解决原始地图与新编地图由于比例尺的变换而产生的地物数量递减问题。

（一）开方根规律的理论依据

开方根规律是一个研究地图上制图物体综合的模式系统。在这个系统中，描述综合程度的所有单个公式都和地图比例尺分母的方根有关。它主要用于选取方面，对形状概括也有一定的意义。

（二）选取规律的通式

1.简单选取规律

\[n_F=n_A\sqrt{\frac{M_A}{M_F}}\]

式中：

\(n_F\):新编地图地物数；

\(n_A\):原始地图地物数；

\(M_F\)新编地图比例尺分母；

\(M_A\)原始地图比例尺分母。

其含义是：新编地图上应当选取的地物的数量可以由原始地图（通常称为资料地图）上的地物数量乘上一个地图比例尺分母之比的根式来求得。

2.开方根规律的扩展

• 通式:

\[n_F=n_AC_zC_s\sqrt{\frac{M_A}{M_F}}\]

式中:

\(C_z\):符号尺度系数

\(C_s\):物体重要系数

• 符号尺度系数

符号尺度满足地图的尺度规律

新编图和资料图上符号相等

符号对不相等也不符合地图的尺度规律

• 物体的重要性系数

物体的重要性也应当影响选取程度。特普费尔认为有三级重要性系数（重要、一般、次要），因此，只确定三个重要性系数。

一般性物体

可按照简单方根规律进行综合的物体称为一般物体，该系数的值为

\[C_s=1\]

这个值代入通式，不会引起任何变化。

重要物体

对地图上被认为必须全部或基本上全部选取的物体称为重要物体，取

\[C_s=\sqrt{\frac{M_F}{M_A}}\]

在暂不考虑符号尺度的条件下，有

\[n_F=n_A\]

次要物体

被认为需要进行比基本方根规律具有更大的综合程度的物体，称为次要物体，取

\[C_s=\sqrt{\frac{M_A}{M_F}}\]

3.公式的简化

开方根选取规律简化公式：

\[n_F=n_A\sqrt{(\frac{M_A}{M_F})^{x}}\]

x=0,  零选取级，\(n_F=n_A\),重要 ，等实地密度

x=1,  第一选取级

\[n_F=n_A\sqrt{\frac{M_A}{M_F}}\]

x=2,  第二选取级

\[n_F=n_A\sqrt{(\frac{M_A}{M_F})^2}\]

x=3,  第三选取级

\[n_F=n_A\sqrt{(\frac{M_A}{M_F})^3}\]

x=4,  第四选取级

\[n_F=n_A\sqrt{(\frac{M_A}{M_F})^4}\]

（三）开方根规律的特点

• 公式直观地显示了制图综合时从重要到一般的选取标
  准，是一个有序的选取等级系统。
• 公式是线性方程，在地图比例尺固定的条件下，地物选取的比例一致。
• 公式的缺憾是没有考虑地理差异，特别是制图地物分布的密度变化。

应用

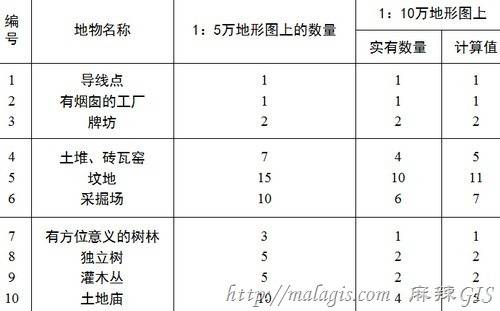
举例：选择面积为100km2的相应地区的1：5万和1：10万地形图的独立地物进行量测试验，量测结果如下：