GIS表示拓扑关系的四元组

二维空间拓扑关系方面Egenhofer等人作出了很好的研究，早期他和Franzosa首先提出了四元组(四交叉：four-intersection)空间拓扑关系形式化描述方法。

二维空间实体点、线、面可以看作是由边界和内部组成的。因此，两实体之间的空间关系可以通过两者的边界和内部的交集是空\(\phi\)或是非空-\(\phi\)来确定。

若\(\partial k\), \(K^0\)表示拓扑空间x的子集k的边界和内部。则对于拓扑空间x的一对子集A和B，它们的边界\(\partial A\)，\(\partial B\)和内部\(A^0\)，\(B^0\)两两之交形成一个由两个简单空间实体点集的边界与边界的交集、边界与内部的交集、内部与边界的交集、内部与内部的交集构成的4×4矩阵的四元组关系SR4（A，B）即为：

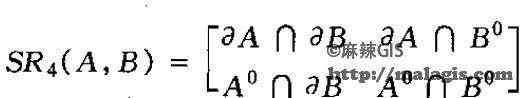
由于四元组中每一交集皆有两种可能性，所以经排列组合有\(2^4\)=16种相互独立的情形，排除掉在现实世界中不具有物理意义的情况，可以得出8种面/面空间关系、16种线/线可能情况、13种线/面可能情况、3种点/线关系、3种点/面关系和两种点/点关系。如下图所示：