基于数值积分的流线生成方法及实现

简介

之前介绍过点图标在三维流场可视化中的一些缺陷，其中之一就是无法揭示数据内在的连续性。所以这里的流线生成算法正好解决这一缺陷，可以提前连续的流线。

流线的构造主要有两种：一种是基于数值积分的流线生成算法，另一种是基于流函数的流线生成算法。基于数值计算的流线构造具有计算简单、符合流体计算中的离散思想。所以这里以之为例。

数值积分的原理

我们假设某一流场中质点的运动规律以速度矢量来描述时可以表示为以下形式：

\[v=v(r,t)\]

其中r为点P的位置向量，为了求出该点P的位置关系随时间t的函数关系，则可以通过求解以下微分方程来得到：

\[\frac{dr(t)}{dt}=v(r(t))\]

求解上述方程，可得：

\[r(t+\Delta t)=r(t)+\int v(r(t))dt\]

对于上述方程所述的曲线，我们不可能用一个显式函数来表示，为了得到该曲线，我们引入数值积分。采用数值积分的思想，我们可以离散成许多离散点来表示曲线。只要我们给定了曲线的起始点，采用数值积分的方法就可以得到\(\Delta t，2\Delta t，3\Delta t …t+\Delta t\)时刻P点的位置，将这些离散点采用直线连接，就可以得到近似的曲线。如图：

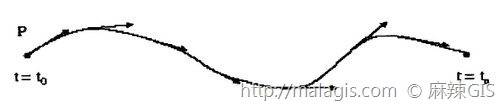
数值积分方式：

一阶Euler方法

\[r(t+\Delta t)=r(t)+v(r(t))\cdot\Delta t\]

这种积分方法，逼近结果比较粗糙，精度也较低。

二阶Runge-Kutta方法

\[r*r(t+\Delta t)=r(t)+v(r(t))\cdot\Delta t\]

\[r(t+\Delta t)=r(t)+1/2[v(r(t))+v(r*(t+\Delta t))]\cdot\Delta t\]

该方法是利用t时刻P点的矢量值和P点在t+\(\Delta \)t时刻的矢量值之和的平均值，作为t时刻的矢量大小，再计算下一点。

四阶Runge-Kutta方法
\[a=v(r(t))\cdot\Delta t\]

\[b=v(r(t)+a/2)\cdot\Delta t\]

\[c=v(r(t)+b/2)\cdot\Delta t\]

\[d=v(r(t)+c)\cdot\Delta t\]

\[r(t+\Delta t)=r(t)+(a+2b+2c+d)/6\]