GIS数据处理-IDL自带函数的巴特沃斯(butterworth)高通/低通滤波
发布时间: 2014-03-10
所属分类: 数字图像处理(IDL)
在之前的文章中,我曾经介绍过IDL实现巴特沃斯(butterworth)高通滤波和IDL实现巴特沃斯(butterworth)低通滤波,不过自己写的套上几重FOR循环,总感觉效率太低。今天介绍的是使用IDL自带的巴特沃斯(butterworth)高通/低通滤波。
下面是冈萨雷斯版本的巴特沃斯(butterworth)滤波器。
巴特沃斯(butterworth)低通滤波器

巴特沃斯(butterworth)高通滤波器

IDL自带巴特沃斯(butterworth)滤波器
\[\frac{1}{\sqrt{1+(\frac{\omega}{\omega_{c}})^{2N}}}\]
从公式以及IDL官方帮助文档里面可以看出这里实现的是一个低通的巴特沃斯。
示例代码
;AUTHOR:尹全超 PRO mybtworth filter = BUTTERWORTH(500,500,CUTOFF=5,/ORIGIN) img = image(filter) END
效果图
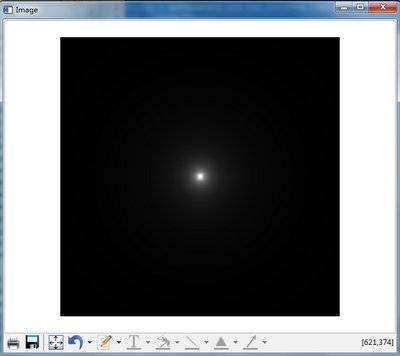
这是一个500*500,截断频率为5的低通滤波器,具体函数原型为:
Result = BUTTERWORTH( X [, Y [, Z]] [, CUTOFF=value] [, ORDER=value] [, /ORIGIN] [, XDIM=value] [, YDIM=value] [, ZDIM=value] )
我看了下相关参数没有关于高通巴特沃斯滤波的实现,于是想了下面的办法。
更新:IDL中,可以通过BUTTERWORTH的ORDER参数控制高通和低通滤波,具体方法见:更新IDL实现巴特沃斯(butterworth)高通滤波,但是下面的方法仍有参考意义。
方法一:整体减去低通,这个用于在具体滤波的时候,乘以原始图像,然后再用原始图像减去低通的图像,剩下的就是高通。
方法二:可以对上面这个公式做一个推导,推导成高通滤波函数,最后结果如下:
高通 = sqrt(1 - 低通 * 低通)
示例代码
;Author: 尹全超 PRO higpassbutterworth filter = BUTTERWORTH(500,500,CUTOFF=100,/ORIGIN) filter = sqrt(1-filter*filter) img = image(filter) END
效果如图
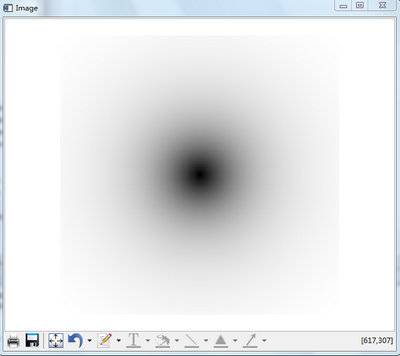
相关阅读
声明
1.本文所分享的所有需要用户下载使用的内容(包括但不限于软件、数据、图片)来自于网络或者麻辣GIS粉丝自行分享,版权归该下载资源的合法拥有者所有,如有侵权请第一时间联系本站删除。
2.下载内容仅限个人学习使用,请切勿用作商用等其他用途,否则后果自负。
手机阅读
公众号关注
知识星球
手机阅读

最新GIS干货

私享圈子





















![[WebGIS] HTML5跟踪GPS轨迹笔记汇总](http://image.malagis.com/pic/gis/2016-09-24_21_12_57_1474722777.75992.jpg?imageView2/1/w/100/h/70)





















