常用地图投影之高斯-克吕格投影(Gauss--Kruger)

高斯－克吕格投影（简称高斯投影）的概念

从几何概念上分析，它是一种横轴等角切圆柱投影。我们把地球看成是地球椭球体，假想用一个椭圆筒横套在其上，使筒与地球椭球的某一经线（称为中央经线）相切，椭圆筒的中心轴位于赤道上，按等角条件将地球表面投影到椭圆筒上，然后将椭圆筒展开成平面。

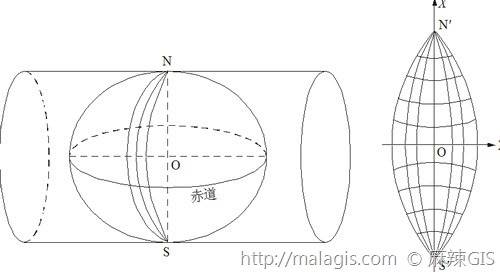
高斯投影的基本条件

• 中央经线和赤道投影成垂直相交的直线
• 投影后没有角度变形，那么经纬线投影后仍正交
• 中央经线没有长度变形

投影的变形分析

其长度比的基本公式为：

\[\mu=1+1/2cos^{2}\phi(1+\eta^{2})\lambda^{2}+1/6cos^{4}\phi(2-tg^{2}\phi) \lambda^{4}-1/8cos^{4}\phi\lambda^{4}\]

长度变形的规律是：

• 中央经线（\(\lambda\)=0）上没有长度变形，即\(\lambda\)=0，\(\mu\)=1
• 同一条纬线上，离中央经线越远变形越大，即\(\lambda\)增大，\(\mu\)也增大
• 在同一经线上,纬度越低，变形越大，即\(\phi\)越小，\(\mu\)越大

投影分带的规定

在1：2.5万到1：50万时，\(6^{0}\)分带

在大于1：1万地形图中：\(3^{0}\)分带

\(6^{0}\)分带法

从格林尼治零度经线起,自东半球向西半球,每经差60分为一个投影带,即东经0～6,6～12,12～18,….174～180,用阿拉伯数字1,2,3,4….60表示投影带号,全球共分为60个投影带。

东半球中央经线的计算公式为:
\[L_{0}=(6n-3)^{0}\]

n表示投影带号，n<30

西半球中央经线的计算公式为:
\[L_{0}=(6n-3)^{0}-360^{0}\]

n表示投影带号，n>30

\(3^{0}\)分带法

从东经\(1^{0}30^{'}\) 算起，自东半球向西半球每\(3^{0}\)为一带，将全球划分为120个投影带，\(1^{0}30^{'}-4^{0}30^{'}\) ,\(4^{0}30^{'}-7^{0}30^{'}\)….其中央经线的位置为\(3^{0},6^{0},9^{0},15^{0}…180^{0},-177^{0}…-3^{0},\)。

坐标网

经纬线网(又称为地理坐标网)

经线和纬线所构成的坐标网,它指示物体在地面上的地理位置。

方里网(直角坐标网)

平行于直角坐标轴的两组直线所构成的方里网格,每隔整公里绘出。在1：10万地形图上直接绘出。

1:5千～1:10万的地形图

经纬线只以图廓线的形式直接表现出来,并在图角处注出相应的度数,在内外图廓间还绘有加密经纬网的加密分划短线(称分度带)。

1:25万～1:100万的地形图

在图面上直接绘出经纬线网。
1:25万    \(\triangle\lambda=15'\)  \(\triangle\phi=10'\)          
1:50万        30'      20'
1:100万       \(1^{0}\)       \(1^{0}\)

方里网(直角坐标网)在≥1：10万的地形图上直接绘出 

我国地形图上方里网密度规定

比例尺     1:5千   1：1万   1：2.5万    1:5万      1:10万
图 上      20 cm    10cm      4cm        2cm        2cm               
实 地       1km      1km      1km        1km        2km

高斯-克吕格投影直角坐标网

1.坐标系的建立

以每个投影带中央经线投影后的直线为X轴,赤道投影后的直线为y轴,其交点为原点。

为了保证y总是>0,将纵坐标轴向西平移500公里

图中A(-334,0),A'(334，0)移轴后,A点的坐标为(166,0), A'(834,0)

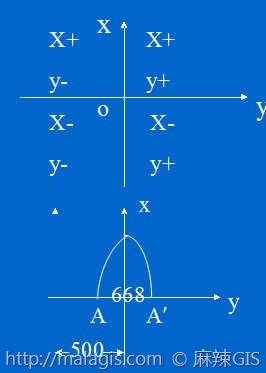
地图上所标出的x,y的值称为通用坐标

x = 3286330(m)        
y = 18 210420

在y坐标里18表示投影带号，210420表示实际坐标（加了500KM）

2.邻带方里网
为什么会产生邻带方里网？

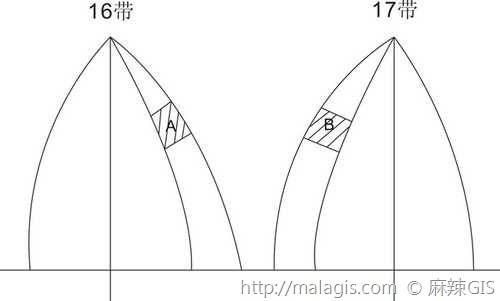
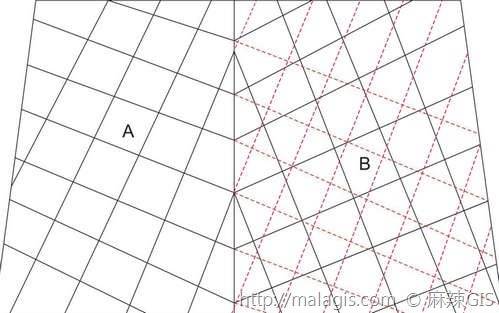
原因：

高斯投影经线收敛于中央经线--相邻带两幅图拼接在一起使用时--两带图幅坐标网之间产生一折角--为了使用方便--在本带某一范围内加绘邻带方里网。

加绘规定

1:2.5万--1:10万

每个投影带西边缘经差30'范围,需加绘前一带的方里网。

每个投影带东边缘一列1:5万(15'),一列1:2.5万(7.5 ')内需加绘东带（后一带）方里网。

1：5000 、1:1万

投影带西边缘经差7.5',即两列1:1万,4列1:5000图上需要加绘邻带方里网。

地图上邻带方里网的表示方法

在外图廓线外绘一短线段