GIS空间数据库（57）空间度量关系

度量关系是在欧氏空间（Euclidean Space）（Blumenthal，1970）和度量空间（Metric Space）（Dhage，1992）上进行的操作，它是一切空间数据定量化的基础。它包含长度、周长、面积、距离等定量的度量关系，其中最主要的度量空间关系是空间对象之间的距离关系。

欧几里德距离定义如下（Kolountzakis and Kutulakos，1992）：

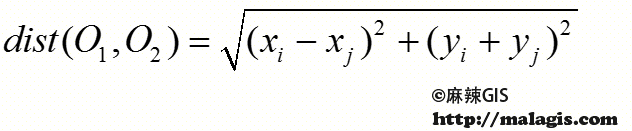
曼哈顿距离是两点在南北方向上的距离加在东西方向上的距离（Wu et al.，1987），即：

点与点之间距离&点与线之间距离

dPL(P,L)=min{d1,d2,…dn}

点与面之间的距离

点P与面A之间有不同的距离概念：“中心距离”是点P与面A中几何中心或者重心之间的距离，“最小距离”是指点P与面A中所有点之间距离的最小值，“最大距离”是指点P与面A中所有点之间距离的最大值。

线与线之间的距离

d(L1,L2)=min{d(P1,P2)|P1∈L1,P2 ∈L2}

线与面之间的距离

线L与面A之间的距离可定义为线L上点PL与面A上的点PA之间距离的最小值。

面与面之间的距离

两个面A1与A2之间的距离可分为三种：“中心距离”是指两个面状物体的质心之间的距离；“最小距离”是指面A1中的点P1与A2中的点P2之间的距离的最小值；“最大距离”是指面A1中的点P1与A2中的点P2之间的距离的最大值。